| Copyright © Klaus Piontzik | ||
| German Version |
| If geomagnetic waves exist, the following conclusion can be drawn: According to Chapter 3.9, equation 3.9.2 applies to all layers of the earth: |
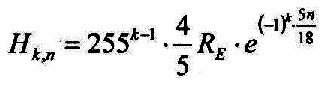
| Let it be: | |
| 6.5.1 Definition | 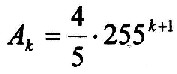 |
| Let it be: | |
| 6.5.2 Definition | 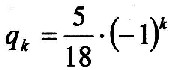 |
| This is how the radial structure can be written in general: |
![]()
| According to Chapter 4.5.1, equation 4.5.1.1, the following applies to the angular component of the field: |
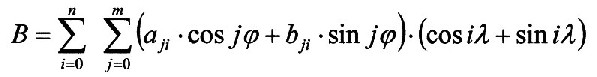
According to chapter 2.11, Equation 2.11.04, the overall solution of the Laplace equation consists of the multiplication of the individual solutions, i.e. the radial component and the angular component. |
| 6.5.1 - Equation: | S(r, λ, φ) = Ak × RE × eqn × B |
| Then, in general, the following equation can be formulated for an earth vibration structure, which also represents a solution to the Laplace equation: |
| 6.5.2 - Equation: |

| The radial component is measured in meters.
The angular component has the unit of measurement Ampere per meter.
So that the units of measurement in the solution function are correct again,
the solution function or the radial component must still be normalized.
The normalized equation then looks like this.
6.5.3 - Equation: |
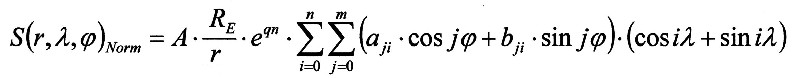
|
This is to be understood as an alternative formulation to Equation 4.1.1 or 4.1.2
by Gauß and Weber, since Equation 6.5.3 more clearly
expresses the layered and oscillatory character of the field.
Whereas the equations of Gauss and Weber describe more of the vector character of the field. The earth's magnetic field plays a central role in the earth's vibration structure. On the one hand, the crystallization of the geological shells led to polyhedral structures in the earth. On the other hand, it is still involved in maintaining the more electrically conductive layers of the atmosphere and thus the earth's electric field. This connection means that the magnetic field is a contributing factor in the formation of weather and climate. |

|
200 sides, 23 of them in color 154 pictures 38 tables Production und Publishing: ISBN 978-3-7357-3854-7 Price: 25 Euro |