	Planetary Systems of the Earth 1 Classisc Systems


	Copyright © Klaus Piontzik


German Version

7.4 - Determination of the approximation line

There are two ways to determine an approximate line from the logarithmic (and linearized) data.

a) through linear regression (without prior linearization)

b) by the existing minimum-maximum values

Case b) will be discussed below, since case a) can be handled using a commercially available calculation program.

We are now looking for the approximation line y = ax + b for the logarithmic values. In the following figure, the approximation line is shown as a dashed line.

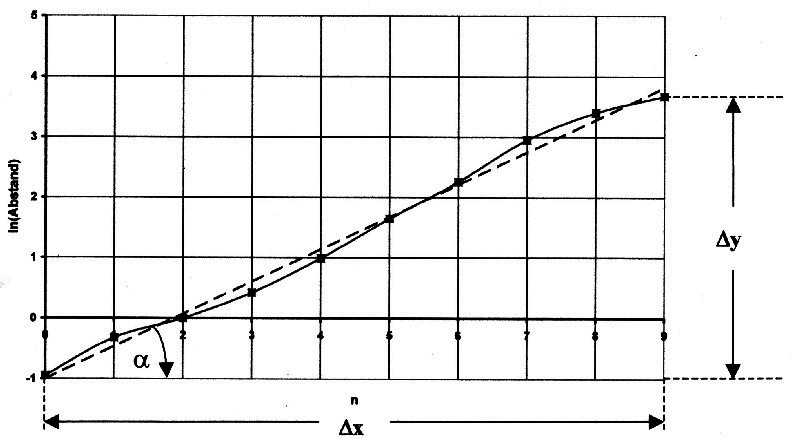
approximation line

Illustration 7.2 approximation line

There are n values ??given, namely: y₀, y₁, y₂, ... y_k, ... y_{_n}

with y_k = ln w_k

There is a minimum y_min and a maximum y_max

The slope a of the approximation line can be determined from the min-max values ??and the new approximate numbering. The following applies:

7.4.1 - Equation:

slope

Δ y is the difference between the minimum and maximum values:

7.4.2 - Equation:

Δ x is the maximum value of the new numbering:

7.4.3 - Equation:

The additive constant of the function you are looking for results from the smallest value:

7.4.4 - Equation:

The following applies to the approximation line:

7.4.5 - Equation:

Inserting all terms gives:

7.4.6 - Equation:

Approximate line total

back

home

next

buy on Amazon

200 sides, 23 of them in color
154 pictures
38 tables

Production und Publishing:
Books on Demand GmbH, Norderstedt

ISBN 978-3-7357-3854-7

Price: 25 Euro