| Copyright © Klaus Piontzik | ||
| German Version |
| Our solar system also has a concentric structure with its planetary orbits. The distances in astronomical units (AU) for the first 8 planets are compiled from the common literature. The individual planets are arranged and numbered according to their distance. |
| Planet | Nr | Distance | ln(Distance) |
| (AU) | |||
Mercury |
0 |
0,3871 |
-0,94907222 |
Venus |
1 |
0,723 |
-0,32434606 |
Earth |
2 |
1 |
0 |
Mars |
3 |
1,524 |
0,42133846 |
Jupiter |
4 |
5,203 |
1,64923538 |
Saturn |
5 |
9,582 |
2,25988634 |
Uranus |
6 |
19,201 |
2,95496236 |
Neptune |
7 |
30,047 |
3,40276282 |
AU = astronomical unit = 149,597,870 km = distance Earth - Sun The table gives the following function y for the logarithms of the distances: |

Illustration 8.2.1 – Logarithmic planetary orbits
| The dashed line in the diagram represents an approximate straight line.
As can be seen, there is already good linearity of the values.
|
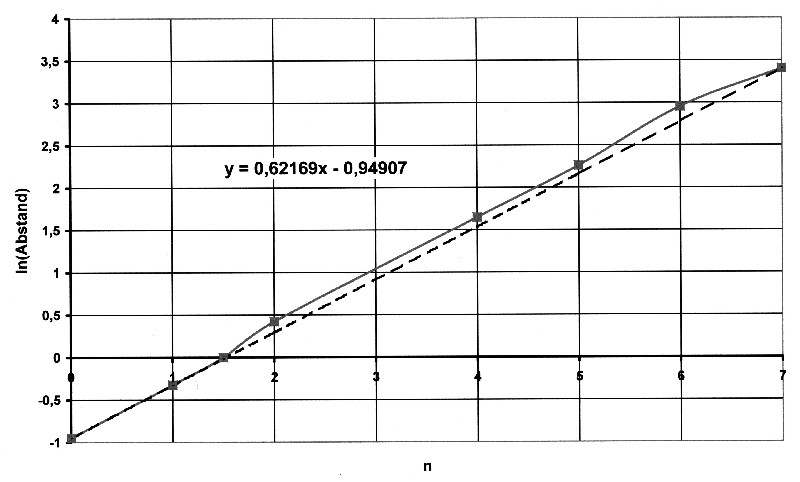
Illustration 8.2.2 – Linearization
| The parameters of the approximation
line are determined using the same procedure as described for the sun shells.
The equation for the approximation line is: y = 0.62169 · x – 0,94907 The following applies to the planetary orbits: Distance = 0.3871 · e0.62169x [AU] This results in the following values: |
| Planet | Nr | Distance | Distance |
| [AU] | [AU] | ||
| calculated | |||
Mercury |
0 |
0,3871 |
0,3871 |
Venus |
1 |
0,723 |
0,7208087 |
Earth |
1,5 |
1 |
0,98359983 |
Mars |
2 |
1,524 |
1,34219887 |
Jupiter |
4 |
5,203 |
4,65383058 |
Saturn |
5 |
9,582 |
8,66577519 |
Uranus |
6 |
19,201 |
16,1363114 |
Neptune |
7 |
30,047 |
30,047 |
The entire situation for the planetary orbits then looks like this:
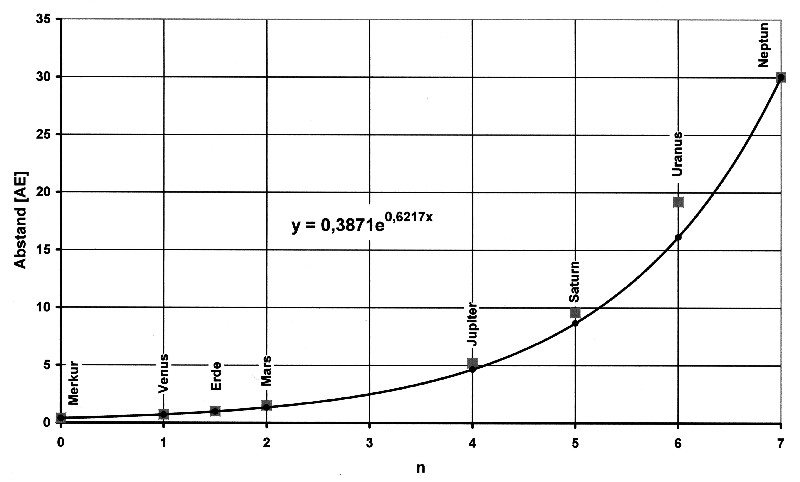
Illustration 8.2.3 – Planetary orbits as an e-function
| The gap for n = 3 is remarkable.
The distance to it is 2.5 AU.
The asteroid belt extends from 2.0 to 3.4 AE. The average is 2.7 AU. The model therefore corresponds very well to real events. And it shows that the asteroid belt is part of the oscillation system of the planets. And it also shows that the procedure of logarithmization and linearization is not an arbitrary act, but rather reveals the harmonic structures of a system. |
| Planet | Nr | Distance | ln(Distance) |
| (AU) | |||
Mercury |
0 |
0,3871 |
-0,94907222 |
Venus |
1 |
0,723 |
-0,32434606 |
Earth |
2 |
1 |
0 |
Mars |
3 |
1,524 |
0,42133846 |
Asteroid belt |
4 |
2,7 |
0,99325177 |
Jupiter |
5 |
5,203 |
1,64923538 |
Saturn |
6 |
9,582 |
2,25988634 |
Uranus |
7 |
19,201 |
2,95496236 |
Neptune |
8 |
30,047 |
3,40276282 |
Pluto |
9 |
39,482 |
3,67584487 |
The table gives the following function for the logarithms of the distances:
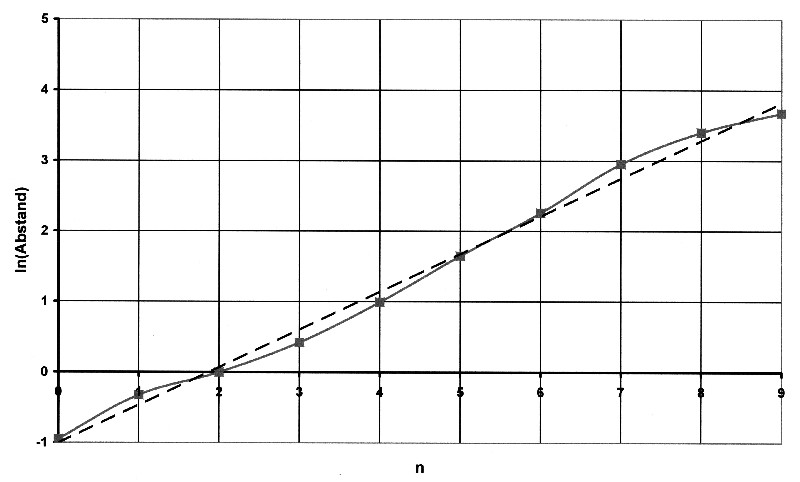
Illustration 8.2.4 – Logarithmic planetary orbits
| The dashed line in the diagram again represents an approximation straight line. As can be seen, there is already a very good linearity behavior of the values. The values ??are linearized and result in the following diagram: |
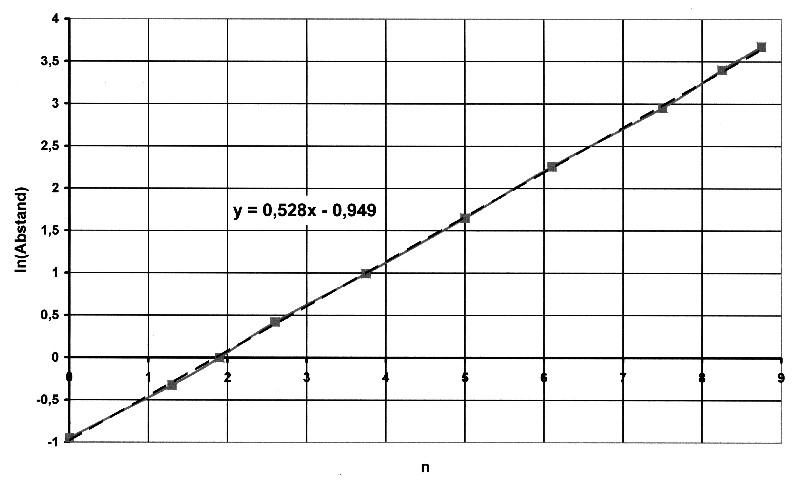
Illustration 8.2.5 – Linearization
| The equation for the approximation line is:
y = 0.52856 · x – 0.94907 The following applies to the planetary orbits: Distance = 0.3871 · e0.52856 · x[AU] This results in the following values: |
| Planet | Nr | Distance |
| new | [AU] | |
Mercury |
0 |
0,3871 |
Venus |
1,3 |
0,723 |
Earth |
1,9 |
1 |
Mars |
2,6 |
1,524 |
Asteroid belt |
3,75 |
2,7 |
Jupiter |
5 |
5,203 |
Saturn |
6,1 |
9,582 |
Uranus |
7,5 |
19,201 |
Neptune |
8,25 |
30,047 |
Pluto |
8,75 |
39,482 |
The new situation for the planetary orbits then looks like this:
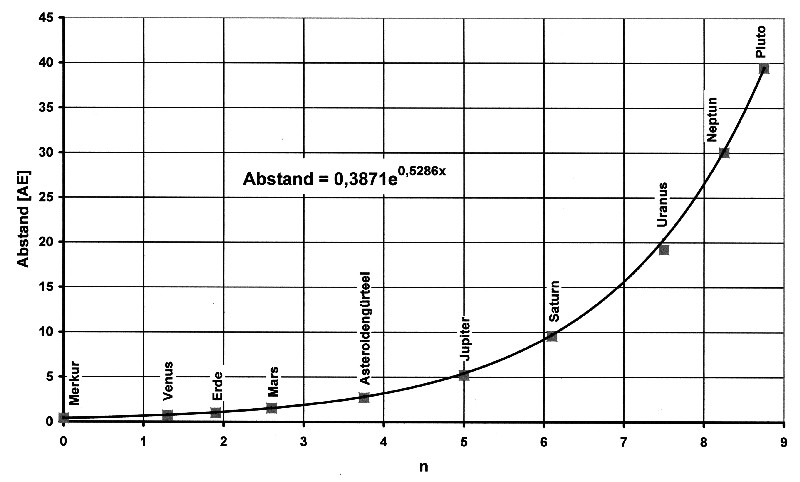
Illustration 8.2.6 – Planetary orbits as an e-function
| There is still the possibility
of better adjustment for the numbering values. Based on the previous linearization,
exact numbers can be calculated, just as was already seen with the sun shells.
The table below shows the calculated numbering values ??as well as the approximate numbers and the initial numbers. |
| Planet | Nr | Distance | Nr | Nr |
| alt | [AU] | calculated | approximately | |
Mercury |
0 |
0,3871 |
0 |
0 |
Venus |
1 |
0,723 |
1,3 |
1,182 |
Earth |
2 |
1 |
1,9 |
1,796 |
Mars |
3 |
1,524 |
2,6 |
2,593 |
Asteroid belt |
4 |
2,7 |
3,75 |
3,675 |
Jupiter |
5 |
5,203 |
5 |
4,916 |
Saturn |
6 |
9,582 |
6,1 |
6,071 |
Uranus |
7 |
19,201 |
7,5 |
7,386 |
Neptune |
8 |
30,047 |
8,25 |
8,233 |
Pluto |
9 |
39,482 |
8,75 |
8,750 |
The more precise function for the planetary orbits is shown in the following illustration 8.2.7
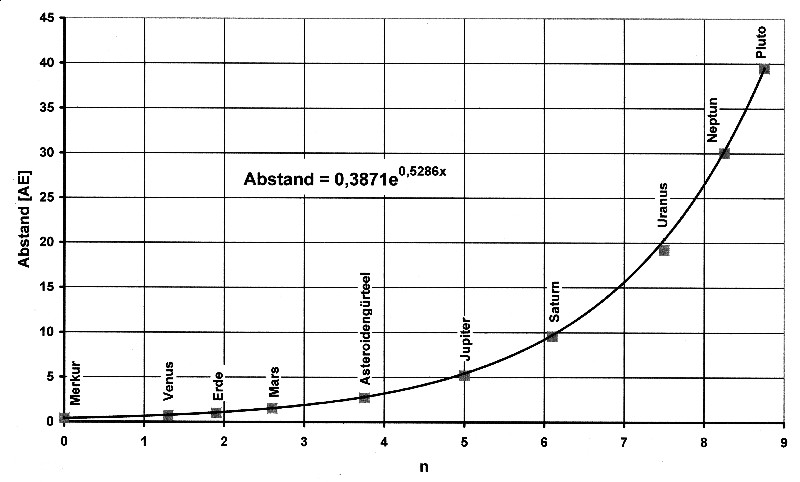
Illustration 8.2.7 – Planetary orbits
| There is a mathematical relationship between orbital radii and orbital times for the planets that also allows the orbital times to be represented as an e-function |
| There is a mathematical relationship between the orbital radii and orbital times of the planets, which Johannes Kepler (*Dec. 27, 1571 - ?Nov. 15, 1630) discovered at the beginning of the 17th century, a German natural philosopher, mathematician, and astronomer. It also allows the circulation times to be represented as an e-function. |
| The general rule is: |
|
| The same applies to Mercury: |
|
By rearranging, the equation for the orbital periods of the planets results:
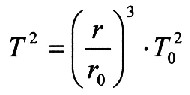
| The following applies: r/r0 = eax und x = calculated numbering |
| Inserting all sizes provides: |
|
|
In 2005, US astronomers discovered a new planet behind Pluto
made of ice and rock. It is the tenth planet in our solar system.
Based on the existing model, the distance to the sun can be determined. The following applies to the planetary orbits: Distance = 0.3871 · e0.52856x[AU] The following applies: x = 10. Based on the previous values, a tolerance of ±0.25 is assumed. This gives the range for the distance of the tenth planet between 67 AU und 87 AU. DThe exact value for x = 10 is 76,44 AE. |

|
200 sides, 23 of them in color 154 pictures 38 tables Production und Publishing: ISBN 978-3-7357-3854-7 Price: 25 Euro |