Approach for an oscillation model

	Planetary Systems of the Earth 1 Classic Systems

	Copyright © Klaus Piontzik


German Version

2.0 - Approach for an oscillation model

The aim of this chapter is the description of basic mathematical and physical terms and conditions, that serve the development of an equation for an oscillation structure and allow a quantification of the model. The approach is based on oscillations around a ball.

Examples for oscillation possibilities:


Sine	Cosine	- Cosine

Illustration 2.0.1 oscillations

sine or cosine = oscillation = wave

Applies to physical oscillations:

2.01 - Equation:

f · λ = c

Frequency multiplied with wavelength is equal to speed of light

How to get vibrations around a ball ? - Analogous to the Bohr model of the atom, if it contains the surrounding Electron as a wave by de Broglie:

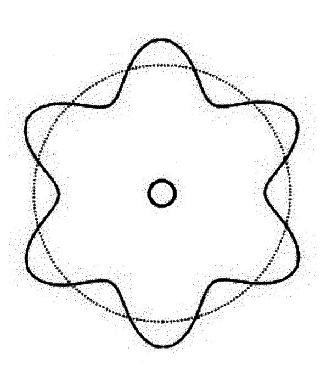
oscillations around a ball

Illustration 2.0.2 oscillations around a ball

It fits only an integer number of oscillations around the globe.

2.02 - Equation:

n·λ ⇔ 360° = 2 · π

n is element of the integers

The wavelength is proportional to the circle angle alpha:

2.03 - Equation:

λ ⇔ α

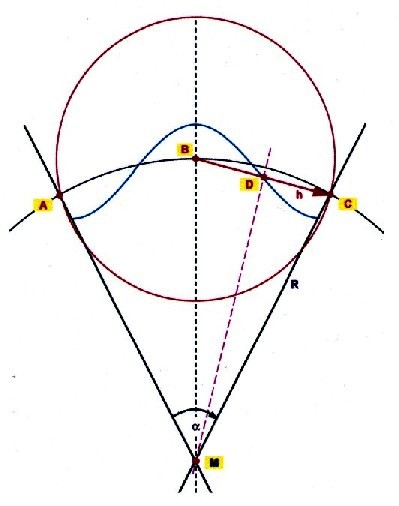
wave length and circle angle

Illustration 2.0.3 wave length and circle angle

Condition for n vibrations around a globe:

2.04 - Equation:

n · α = 2 · π

n is element of the integers

Theoretically, the following form is possible:

2.05 - Equation:

n · α = 2 · π · m

m, n are elements of the integers

Here, the oscillation circle does not close after one revolution, but only take m turns.

back

home

next

Planetare Systeme 1

buy on Amazon

200 sides, 23 of them in color
154 pictures
38 tables

Production und Publishing:
Books on Demand GmbH, Norderstedt

ISBN 978-3-7357-3854-7

Price: 25 Euro