| Copyright ©: Klaus Piontzik | ||
| German Version |
2.1 - Spherical harmonics
| A standing wave
around a sphere can be interpreted as a stationary state.
Thus, each state of a wave is spatially fixed. The
question now is: how many waves fit around a globe? In classical mechanics, degrees of freedom is the number of freely selectable, independent movements of a system A rigid body in space has a degree of freedom f = 6, because you can move the body in three independent directions and rotate in three independent planes. Because a sphere is rotationally symmetric, so rotations are irrelevant. A ball has therefore 3 freedoms regarding a wave propagation. Therefore, 3 inde-pendent waves around the globe are possible. Due to the spherical shape, the three freedoms can be represented as spherical coordinates. Example earth: 1) A wave starts from North Pole via the South Pole to the North Pole 2) The second wave runs around the equator 3) The third standing wave runs radially - based from the center There exists a mathematical concept namely for the first two examples, that is suitable for a representation - the spherical harmonics. Standing waves on the surface of a sphere can be treated as spherical harmon-ics. There are 3 types: |
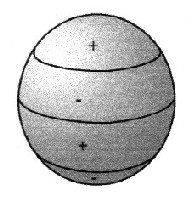 |
Zonal spherical harmonics
only depend on the latitude sin φ cos φ |
|
| Illustration 2.1.1 - zonal spherical harmonic | ||
 |
Sectorial spherical
harmonics depend only by the degree of longitude sin λ cos λ |
|
| Illustration 2.1.2 - sectorial spherical harmonic | ||
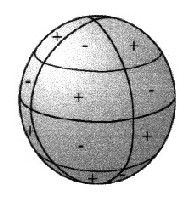 |
Tesseral spherical
harmon-ics depend of the latitude and
the longitude sinφĚsinλ sinφĚcosλ cosφĚsinλ cosφĚcosλ |
|
| Illustration 2.1.3 - tesseral spherical harmonic |
| 2.1.1 - Definition: | tesseral spherical harmonic = product of two oscillations of 2 perpendicular standing waves = grid |
| Comment: A complete route in terms of square grid on a sphere can not materialize. Only grid systems are developed, which are designed as the geographic grid system. There are always two poles. The corresponding "meridians" and "circle of latitude" then make the grid. |

|
200 sides, 23 of them in color 154 pictures 38 tables Production und Publishing: ISBN 978-3-7357-3854-7 Price: 25 Euro |