| Copyright © Klaus Piontzik | ||
| German Version |
| Following general solution function is specified for the part of the angle: |
| Equation 2.11.1.1 | 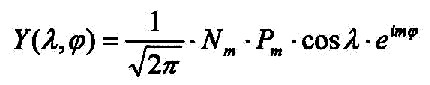 |
| These are the spherical harmonics in complex notation. |
| The Euler equation applies: | ei·mφ = cos(m·φ) + i·sin(m·φ) |
|
The Nm
and Pm
are the so called Legendre polynomials,
which can be manipulated like constants
in our consideration.
So results total: |
|
|
|
|
|
|
| And here you can see again the multiplicative associated sine and cosine functions, so tesseral spherical harmonics or grids. Here equipped with a real and an imaginary part, so a complex function as a general solution for the angle part of the Laplace's equation.. |

|
200 sides, 23 of them in color 154 pictures 38 tables Production und Publishing: ISBN 978-3-7357-3854-7 Price: 25 Euro |