| Copyright © Klaus Piontzik | ||
| German Version |
| With the
construction of the spatial oscillation structure a
mathematical and physical model is available that allows
to explain the structures of the earth on a basis
of waves. The question is: What is a
general approach for an oscillation structure? Pierre-Simon
(Marquis de) Laplace (28.03.1749 bis 05.03.1827)
was a French mathematician, physicist, and astronomer. He
worked in the fields of probability theory and
differential equations. The Laplace operator Nabla is a mathematical operator that is a general mathematical provision (calculation way). The Laplace operator is a differential vector operator within the multidimensional analysis. The Laplace operator occurs in Laplace's equation, for example. Twice continuously differentiable solutions of this equation are called harmonic functions. |
| Laplace equation: |
| Equation 2.11.01 | |
| to be read: Nabla f is zero |
Expressed in cartesian coordinates (x, y, z):
| Equation 2.11.02 | 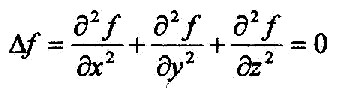 |
Applies in only one dimension:
| Equation 2.11.03 | 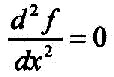 |
| This is
the equation for a harmonic oscillator,
such as a pendulum or a spring without friction. The Laplace's equation represents a mathematical formula to describe oscillation phenomena in space. The common approach to a solution with a central configuration is to transform the Cartesian coordinates (x, y, z) in spherical coordinates (lambda, phi, r). Then, the entire function is decomposed into two part functions. Where a function the radial part contains and the other function the part of the angle. The general approach to a solution function of Laplace's equation in spherical coordinates looks like this: |
| Equation 2.11.04 | 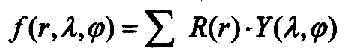 |
Both
part functions R and Y can be solved in
each case individually.

|
200 sides, 23 of them in color 154 pictures 38 tables Production und Publishing: ISBN 978-3-7357-3854-7 Price: 25 Euro |