| Copyright © Klaus Piontzik | ||
| German Version |
| According to chapter 2.1 a ball
has three degrees of freedom f = 3. Two
degrees of freedom could be covered through the use of
spherical harmonics The third freedom, the radial direction, is still missing. This requires the under-standing of a physical representation with which the expansion of physical waves can be described: the Huygens-Fresnel principle. The huygensche principle emanates from a source S, which generate wave fronts uniformly in all directions. To get the resulting wave front in the point P, it is not necessary to consider the entire spread of S. The Huygens-Fresnel principle says that every point (O) from a wavefront can be considered as a starting point of a new wave, the so-called elementary wave. The location of the resulting wavefront in P arises from superposition of all elementary waves. |
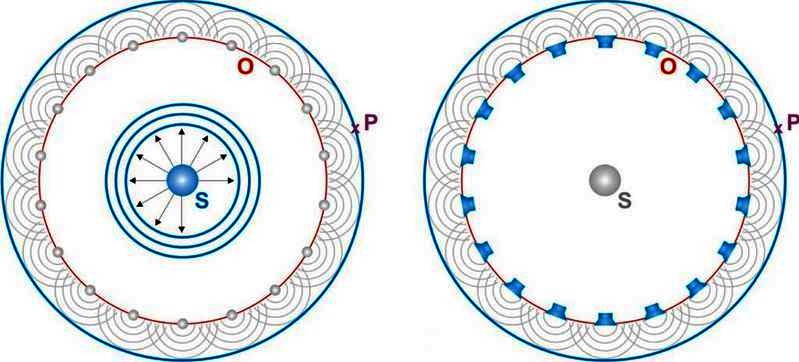
| Illustration 2.3.1 – Huygens-Fresnel principle |
| The origins of the waves
(O) deliver the resulting wave front (P)
by superposition of elementary waves.
In two dimensions, elementary waves are circular. In three dimensions, elementary waves are spherical in shape. |
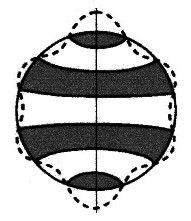 |
Application of the
Huygens-Fresnel principle for a standing wave around a
globe: Extreme values of the wave = sources = waves origins 1 wave = 2 sources |
| Illustration 2.3.2 – wave origins |
| The following image shows the oscillation state for a wave by the Huygens-Fresnel principle with a maximum (wave peak) as a source. |
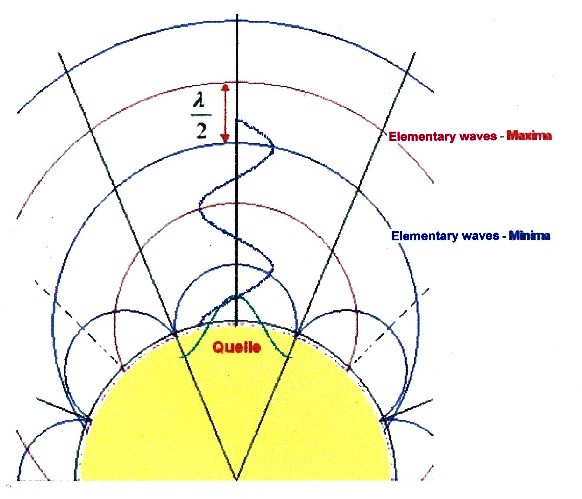 |
| Illustration 2.3.3 – elementary waves |
| Since a wave consists of maxima and minima, the elementary waves also form minimal fronts (blue) and maximum fronts (red). Between the extreme fronts course zero fronts exist. |

|
200 sides, 23 of them in color 154 pictures 38 tables Production und Publishing: ISBN 978-3-7357-3854-7 Price: 25 Euro |