| Copyright © Klaus Piontzik | ||
| German Version |
| The earth with their geological layers and the
atmosphere layers represent solutions of the radial component of Laplace's equation, resulting in oscillation phenomena.
. According to equation 3.6.4 it can be written in general for the geological layers: |
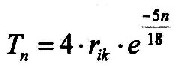
| According to equation 3.8.3 it can be written in general for the atmospheric layers: |
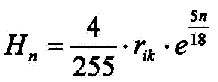
| So it be: k=0 for atmospheric layers k=1 for geological layers Then applies to all layers of the earth: |
| 3.9.1 - Equation: | 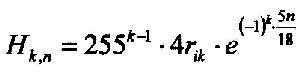 |
[Km] |
| with rik = RE/5
und rik
= inner core and RE =
6371 Km you can also write: |
| 3.9.2 - Equation: | 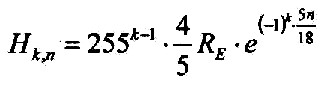 |
[Km] |
| For the geologic and the atmospheric layers it was shown in two things way that it is an oscillation phenomena: : |
| a) direct comparison with calculated layers b) as a solution of the radial part of Laplace's equation |
| The geological and the atmosphere layers are therefore planetary systems with an oscillation structure. |
| 3.9.3 - Definition: | Planetary oscillation system = Planetary system with an oscillation structure |
| 3.9.4 - Theorem: | The structure of the two planetary oscillation systems, the geological layers and the atmospheric layers, are represented by a single oscillation structure. |
| 3.9.5 - Theorem: | Earth layer ⊂ Laplace solution ⊂ Earth oscillation structure |
| Generally the following statement can be generated: |
| 3.9.6 - Satz: | Stratification around or in a central solid is always the expression of an oscillation phenomenon. |
|
Geological layers, atmospheric layers and also electrons
on their orbitals around the nuclei obey the same laws of oscillation,
resulting from Laplace's equation. Here the question originates whether this oscillation principle is, much more of a general nature and arises here as a structural principle of the universe? |