| Copyright © Klaus Piontzik | ||
| German Version |
|
From the school and from the media, we always know the
earth's magnetic field as a field that corresponds to the field of
a bar magnet. It is due to the so called dipole field.
Historical this view of the earth's magnetic field explains the behavior of a needle of in-clination. For historical reasons, this view of the magnetic field explains the behavior of an inclination needle. The needle is perpendicular to the earth's surface at the pole and horizontal to the earth's surface at the equator. |
|
| Illustration 4.0.1 – dipole field |
| Taking measured values of the field, ít can be shown graphically that four magnetic poles (Illustration 3.4.2) exist and that the dipole model is not sufficient to explain exactly the real earth's magnetic field. |
|
The physical approach for such
a dipole field is the con-templation of the magnetic field of a so called current loop. The mathematical derivation leads to a differential equation in which a so-called elliptic integral occurs, for which no closed mathematical solution - in the form of an equation - exists. |
|
| Illustration 4.0.2 – current loop |
| The mathematically commonly used approach
is converting the appearing term in the integral in an infinite sequence: Simplified can be written: |
![]()
| Then just cut off this sequences after the first link. Now integrate the rest, so the general equation for the dipole field, which only depends on the geographical latitude φ is created. |
| 4.0.1 - Equation: | 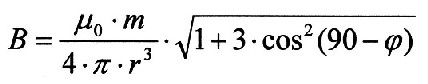 |
µ T |
| In the equation stands: B for the magnetic flux density φ for the latitude m for the magnetic moment r for the Earth's radius µ for die magnetic permeability m, r, µ are constants that are defined as follows: The magnetic moment in this case is the earth's magnetic moment with m = 6.6845*1022
Am2 For the earth's radius you take
the value from a geodetic system, in this case the WGS84 The magnetic permeability µ = 10-7 Vs/Am (For the derivation of the dipole field see also "Berkeley Physics Course 2" by Edward Purcell, pages 266-269) |
| The mathematical approach presented here to the achievement
of the dipole equation can be considered due to the cut off limbs of the rest,
merely as a first approximation.
If you start to integrate the remaining limbs of the infinite sequence (from the current loop consideration), so you get the quadrupole field, the Octupole field, etc. Overall, this is called multi pole forming. |
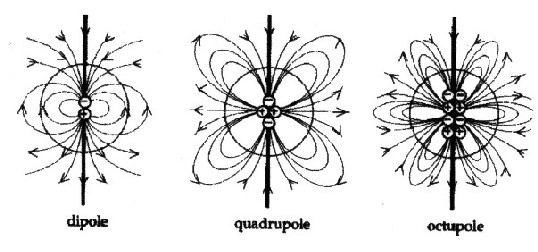
| Illustration 4.0.3 – multi pole forming |
| See "Grid Structures of the Earth's Magnetic Field," Chapter 1, The Earth's Dipole Field, pages 17-23. |

|
200 sides, 23 of them in color 154 pictures 38 tables Production und Publishing: ISBN 978-3-7357-3854-7 Price: 25 Euro |