| Copyright © Klaus Piontzik | ||
| German Version |
| Already Gauß and Weber recognized in 1838,
in their experiments with the earth's magnetic field, that the magnetic field can not be
explained just by the model of a rod magnet or a current loop.
In 1838 appeared the "general theory of terrestrial magnetism" of C.F. Gauß and W. Weber where they specify the following potential equation for the magnetic field of the earth: 4.1.1 - Equation: |
|
 |
|
|
|
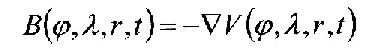 |
| According to equation 4.1.2 the magnetic flux density B is depending on the latitude φ, the longitude λ, distance r from the center and the time t. |
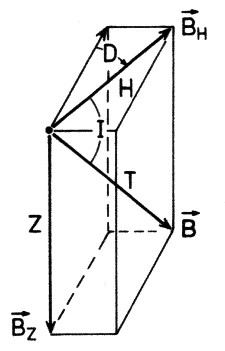 |
The so called field elements of the magnetic field can be generated from this vector.
So, the declination, the inclination and the total intensity etc. |
| Illustration 4.1.1 – field elements |
| The equations of Gauß and weber for the earth magnetic field are used till this day.
From the potential equation or also the theory the really appearing coefficients cannot be determined in the potential equation. This happens about a measurement of the real magnetic field of the earth. Remark: If you remove the brackets in the potential equation, only products of sine or cosine functions, i.e. tesseral spherical surface functions or lattices, appear in Gauss' equation. That means: Gauss and Weber already based their observations on the earth's magnetic field on spherical surface functions!!! See also "Grid structures of the earth's magnetic field", Chapter 2.7, Gauss' approach, pages 32-33. |

|
200 sides, 23 of them in color 154 pictures 38 tables Production und Publishing: ISBN 978-3-7357-3854-7 Price: 25 Euro |