| Copyright © Klaus Piontzik | ||
| German Version |
| The approach here shall find an oscillation base for the earth's magnetic field. It exists a mathematical method, namely the Fourier analysis. With it a given periodic function can be decomposed as a sum of sine and cosine functions |

| Illustration 4.5.1 – total intensity |
| The illustration 4.5.1 is converted into a table of total intensities.
And so, the possibility of an evaluation is given. Also a 3D representation of the earth's magnetic field at the earth's surface is possible. Here, the evaluation is made via a two-dimensional Fourier analysis. A Fourier analysis provides a decomposition of a given function as a sum of sine and cosine functions. A two-dimensional Fourier analysis receives a sum of spherical harmonics. And with the earth's magnetic field actually can be made a decomposition into spherical harmonics. |
| The total field is decomposed into single - in this case horizontal - cuts. With each cut, a one-dimensional Fourier analysis can be done.
Each section runs along a parallel. The cuts are created by +90 North to -90South at a distance of 7.5 degrees. The results are 25 sections. (7.5 Degrees = 800 km) Considering a one-dimensional (numeric) Fourier analysis to every cut with the variable λ and the step of 7,5 degrees, i.e. with 48 points per cut. There are total 1106 Points for the analysis of the earth's field. A numeric (one-dimensional) harmonic procedure serves as a basis, or an analysis tool, as described in the book "Mathematics for engineers" by Brauch/Dreyer/Haacke and as Algorithm of Goertzel (and Reinsch) is known. Then, the 25 slices from the Fourier analysis generally can be represented: |
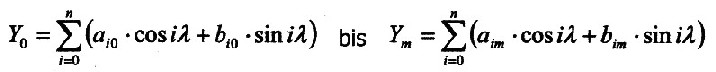
|
The result is a system of equations with m+1 equations with each n+1 elements.
The generated coefficient matrix with the Am and Bm can be performed as one more Fourier analysis, with the variable φ. Every point on the earth with the coordinates φ, λ qualifies as: A further Fourier analysis can be carried out with the variable φ using the generated coefficient matrix with and for every point on earth with the coordinates λ, φ the following applies: |
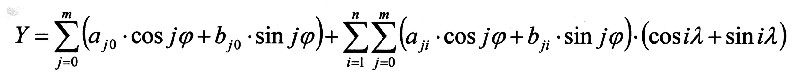
| The entire Fourier analysis process then looks like this: |

| The first term for Y (the zonal, sectorial part) can be still complemented so: |
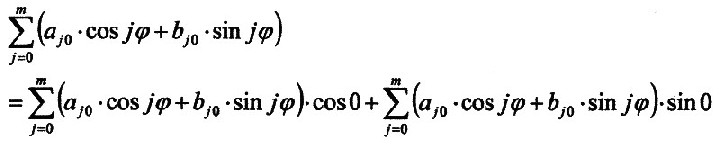
|
Due to the quantitative analysis on the one hand and
the mathematical methods, on the other hand, the following
total equation for the magnetic flux density at the earth's surface can be created:
4.5.1.1 - Equation: |

| If you remove the brackets behind the double sum, only tesseral spherical surface functions i.e. b>lattices, appear. |
| 4.5.1.2 - Theorem: | The magnetic field of the earth (on the earth surace) can be completely described by a sum of grids. |
| At the same time, this function represents a solution of the angle part of La-place's equation. In the consequence is then: |
| 4.5.1.3 - Theorem: | Magnetic field of the Earth (on the surface)
= two-dimensional oscillation structure |
| Here arises the question whether there is a relation between the two-dimensional magnetic oscillation model and the earth oscillation structure?
Because of the general approach of the Fourier analysis and of the equation 4.5.1.1 the following general statement can be made: |
| 4.5.1.4 - Theorem: | Each oscillation structure on or around a sphere can e completely described by a sum of tesseral spherical harmonics. |
| Considering the statements and equations in chapter 2.11.1 the following can be said: |
| 4.5.1.5 - Theorem: | Each oscillation phenomenon around a sphere can be represented as a solution of the angular part of the Laplace equation. |

|
200 sides, 23 of them in color 154 pictures 38 tables Production und Publishing: ISBN 978-3-7357-3854-7 Price: 25 Euro |